目录
我们知道,单位四元数 q 和 so(3) 向量 $\boldsymbol\phi$ (即 rotation vector)的对应关系为:
${\bf q}({\boldsymbol \phi}) = [ \sin\frac{\phi}{2} {\bf a}, \, \cos \frac{\phi}{2}]’$, in which $\phi = | \boldsymbol \phi|, \, {\bf a} = \frac{\boldsymbol \phi}{\phi} $
当 $\phi$ 很小时,可以近似表达为:
\[{\bf q}({\boldsymbol \phi}) = [ \frac{1}{2} {\bf \boldsymbol \phi}, \, 1]'\]四元数小量和李代数小量有很简单的对应关系,所以在使用四元数的优化问题中,往往也取 $\delta\boldsymbol \phi$ 小量作为更新量,例如 OKVIS [1]。
具体到优化过程中,使用李群李代数(如预积分论文 [2])和使用四元数之间还是有区别的。使用李群李代数,在 residual 推导时会用到 so3 的左雅可比或右雅可比;使用四元数,会用到四元数矩阵(或共轭四元数矩阵)。不过既然两者使用的小量一致,那四元数矩阵和 so3 的左右雅可比的关系如何呢?
之所以有这个疑问,是因为 Xingyin 兄在博客里指出 [3],OKVIS 代码中使用了预积分,代码和预计分论文里的思路一致。不过实际上,虽然预积分流程一致,两者在雅可比推导上有所不同:预积分使用 so3 的右雅可比;OKVIS 使用四元数矩阵。所以,我们有必要把这两者的关系厘清。
四元数矩阵
两个旋转叠加,可以表达为两个四元数相乘,或者一个 4*4 矩阵与一个四元数相乘:
\[{\bf q} \otimes {\bf p} = \begin{bmatrix} q_w p_x - q_z p_y + q_y p_z + q_x p_w \\ q_z p_x + q_w p_y - q_x p_z + q_y p_w \\ -q_y p_x + q_x p_y + q_w p_z + q_z p_w \\ -q_x p_x - q_y p_y - q_z p_z + q_w p_w \\ \end{bmatrix} = {\bf Q}_l({\bf q)p} = {\bf Q}_r{\bf (p)q}\]这里的 ${\bf Q}_l$ 为四元数矩阵, ${\bf Q}_r$ 为共轭四元数矩阵:
\[{\bf Q}_l({\bf q}) = \begin{bmatrix} q_w {\bf I}_3 + {\bf q}_{1:3}^\wedge & {\bf q}_{1:3}\\ - {\bf q}_{1:3}' & q_w \end{bmatrix} , {\bf Q}_r ({\bf q}) = \begin{bmatrix} q_w {\bf I}_3 - {\bf q}_{1:3}^\wedge & {\bf q}_{1:3}\\ - {\bf q}_{1:3}' & q_w \end{bmatrix}\]两种矩阵对于求导非常方便:
\[\frac{\partial{\bf q \otimes p}}{\partial\bf p} = {\bf Q}_l({\bf q}), \,\frac{\partial{\bf q \otimes p}}{\partial\bf q} = {\bf Q}_r ({\bf p})\]现在,假设有个一个待估计的旋转量 q ,其更新方式为 $\bf q \leftarrow q \otimes q(\boldsymbol\alpha)$ , $\boldsymbol \alpha$ 为 so3 小量。假定有 q 的测量量 $\bf\tilde q$,定义误差函数 ${\bf e}_{\rm qt}$ :
\[{\bf e}_{\rm qt} = 2( \tilde {\bf q}^{-1}\otimes {\bf q})_{1:3}\]则其相对于更新量的雅可比为
\[\begin{aligned} \frac{\partial {\bf e}_{\rm qt}}{\partial \boldsymbol \alpha} &= 2\frac{\partial (\tilde{\bf q}^{-1}\otimes{\bf q}\otimes {\bf q}({\boldsymbol \alpha}))}{\partial \boldsymbol \alpha}\Bigg | _{(1:3, :)} \\ &=2\frac{\partial (\tilde{\bf q}^{-1}\otimes{\bf q}\otimes {\bf q}({\boldsymbol \alpha}))}{\partial {\bf q}({\boldsymbol \alpha})} \frac{\partial {\bf q}({\boldsymbol \alpha})}{\partial \boldsymbol \alpha}\Bigg | _{(1:3, :)} \\ &={\bf Q}_l(\tilde{\bf q}^{-1}\otimes{\bf q}) \begin{bmatrix} {\bf I}_3 \\ {\bf 0_{1\times 3}} \end{bmatrix}\Bigg | _{(1:3, :)} \\ &={\bf Q}_l(\tilde{\bf q}^{-1}\otimes{\bf q}) _{(1:3, 1:3)} \end{aligned}\]即 $\frac{\partial {\bf e}_ {\rm qt}}{\partial \boldsymbol \alpha} ={\bf Q}_ l[{\bf q}({\bf e}_{\rm qt})] _{(1:3, 1:3)}$
so(3) 雅可比
据 Barfoot [4],若 $\boldsymbol\phi$ 的左雅可比为 ${\bf J}_l({\boldsymbol \phi})$ ,右雅可比为 ${\bf J}_r({\boldsymbol \phi})$ :
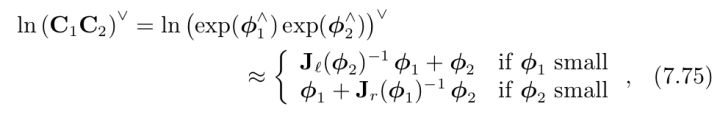
于是,假设有待估计量 C,更新方式为 ${\bf C} \leftarrow {\bf C}\, {\rm Exp}({\boldsymbol \alpha})$ , $\boldsymbol \alpha$ 为 so3 小量。假定有 C 的测量量 $\bf\tilde C$,定义误差函数 ${\bf e}_{\rm lie}$ :
\[{\bf e}_{\rm lie} = {\rm Log}( \tilde {\bf C}' {\bf C})\]则其相对于更新量的雅可比为:
\[\begin{aligned} \frac{\partial {\bf e}_{\rm lie}}{\partial \boldsymbol \alpha} &= \frac{\partial{\rm Log}(\tilde{\bf C}'{\bf C} \,{\rm Exp} ({\boldsymbol \alpha}))}{\partial \boldsymbol \alpha} \\ & = {\rm J}_r({\rm Log(\tilde{\bf C}'{\bf C} )})^{-1}\\ & = {\rm J}_r({\bf e}_{\rm lie})^{-1} \end{aligned}\]讨论
我们来比较一下 $\frac{\partial {\bf e}_ {\rm qt}}{\partial \boldsymbol \alpha}$ 和 $\frac{\partial {\bf e}_{\rm lie}}{\partial \boldsymbol \alpha}$。
首先,
\[\begin{aligned} \frac{\partial {\bf e}_ {\rm qt}}{\partial \boldsymbol \alpha} &={\bf Q}_l[{\bf q}({\bf e}_{\rm qt})] _{(1:3, 1:3)}\\ &=q_w({\bf e}_{\rm qt}) {\bf I}_3 + {\bf q}_{1:3}^\wedge({\bf e}_{\rm qt}) \end{aligned}\]如果可以认为误差函数 ${\bf e}_{\rm qt}$ 很小,则
\[\frac{\partial {\bf e}_{\rm qt}}{\partial \boldsymbol \alpha} \approx {\bf I}_3 + \frac{1}{2}{\bf e}_{\rm qt}^\wedge\]另一方面,据 Barfoot [4],有
\[\frac{\partial {\bf e}_{\rm lie}}{\partial \boldsymbol \alpha} = {\rm J}_r({\bf e}_{\rm lie})^{-1} = \frac{\phi_{e}}{2}\cot\frac{\phi_{e}}{2} {\bf I}+(1-\frac{\phi_{e}}{2}\cot\frac{\phi_{e}}{2}){\bf a_{\it e}a_{\it e}}' + \frac{\phi_{e}}{2}{\bf a}_{e}^\wedge\]如果可以认为误差函数很小,即 $\phi_{e}\rightarrow 0$ ,则 $\frac{\phi_{e}}{2}\cot\frac{\phi_{e}}{2} \rightarrow 1$ ,于是
\[\frac{\partial {\bf e}_{\rm lie}}{\partial \boldsymbol \alpha} \approx {\bf I}+\frac{\phi_{e}}{2}{\bf a}_{e}^\wedge={\bf I} + \frac{1}{2}{\bf e}_{\rm lie}^\wedge 。\]可以看到,当可以认为误差函数很小时, $\frac{\partial {\bf e}_ {\rm qt}}{\partial \boldsymbol \alpha}$ 和 $\frac{\partial {\bf e}_ {\rm lie}}{\partial \boldsymbol \alpha}$ 是相等的。这其实很好理解,因为当 ${\bf e}_ {\rm qt} = 2( \tilde {\bf q}^{-1}\otimes {\bf q})_ {1:3} $ 很小时,${\bf q}({\boldsymbol \phi}) = [ \frac{1}{2} {\bf \boldsymbol \phi}, \, 1]’$ 估计成立,所以 ${\bf e}_ {\rm qt}, {\bf e}_{\rm lie}$ 实际上就表示同一个量,都是误差旋转量的李代数,推导出来的雅可比自然就一样了,我们只是通过不同的途径去算同一个量而已。这个例子的价值在于,展示了四元数矩阵和 so3 雅可比之间的具体关系,即:
如果有可以认为很小的 so3 量,如某个误差函数 ${\bf e}_ {\phi}$ ,则 ${\bf J}_ r({\bf e}_ {\phi})^{-1} = {\bf Q}_ l({\bf q}({\bf e}_ {\phi})) _{(1:3,1:3)}$
上面用的是右扰动模型;如果使用左扰动,可类似地得到 ${\bf J}_ l({\bf e}_ {\phi})^{-1} = {\bf Q}_ r({\bf q}({\bf e}_ {\phi}))_ {(1:3,1:3)}$ 。
尾声
如果 $\phi$ 不能认为很小,${\bf J}_ r(\boldsymbol \phi)^{-1}$ 与 ${\bf Q}_ l({\bf q}( {\boldsymbol\phi} ))$ 的关系是怎样?并不复杂。区别仅在于此时 ${\bf q}({\boldsymbol \phi}) = [ \frac{1}{2} {\bf \boldsymbol \phi}, \, 1]’$ 的估计不能成立,$ 2{\bf q}_ {1:3}$ 和 $\boldsymbol \phi$ 不能当作一个量而已;但它们之间的相互关系是已知的:${\bf q}_{1:3}= \sin\frac{|\boldsymbol\phi|}{2} \cdot \frac{\boldsymbol \phi}{|\boldsymbol\phi|}$。在上面的演算中,我们实际上得到的结果是
\[\frac{\partial\boldsymbol \phi}{\partial{\boldsymbol \alpha}}={\bf J}_r({\boldsymbol\phi})^{-1},\quad \frac{\partial{\bf q}_{1:3}}{\partial{\boldsymbol \alpha}}={\bf Q}_l({\bf q}({\boldsymbol\phi}))_{(1:3,1:3)}\]可以证明:
\[{\bf J}_r({\boldsymbol\phi})^{-1} = \frac{\partial\boldsymbol \phi}{\partial{\bf q}_{1:3}} \,{\bf Q}_l({\bf q}({\boldsymbol\phi}))_{(1:3,1:3)}\]代入过程就不贴了。
参考文献
[1] S. Leutenegger, S. Lynen, M. Bosse, R. Siegwart, P. Furgale, “Keyframe-based visual-inertial odometry using nonlinear optimization”, Int. Journal of Robotics Research (IJRR), 2014.
[2] C. Forster, L. Carlone, F. Dellaert and D. Scaramuzza, “On-Manifold Preintegration for Real-Time Visual–Inertial Odometry,” in IEEE Transactions on Robotics, vol. 33, no. 1, pp. 1-21, Feb. 2017.
[4] T. Barfoot, State Estimation for Robotics.